1. Введение

Рейтинг сегодня является непременным атрибутом любого шахматиста достаточно высокого класса. По рейтингу встречают – по рейтингу провожают. Высокий рейтинг дает право на участие в турнирах высших категорий (да и сами категории турниров определяются по среднему рейтингу их участников), а следовательно, и возможность претендовать на высокие гонорары. Достижение определенного уровня рейтинга является необходимым условием получения мастерского или гроссмейстерского звания. Рейтинг участника (или средний рейтинг команды) учитывается при жеребьевке соревнований, проводимых по швейцарской системе. Более высокий рейтинг соперников обеспечивает и более высокое место при равенстве набранных в турнире очков. Молодые шахматисты стремятся поскорее получить свой начальный рейтинг, а шахматисты, возглавляющие рейтинг-лист, минимизируют число соревнований или тщательно отбирают их, чтобы не подвергнуться риску покинуть свое почетное место. Несвоевременное перечисление федерацией денег за обсчет рейтинга может стать трагедией для шахматистов целой страны, лишив их права участия в профессиональных турнирах. Пожалуй, еще только в профессиональном теннисе спортсмены так же бережно и ревностно относятся к своему рейтингу, как и поклонники Каиссы.  Итак, рейтинг – это явление (со своими достоинствами, недостатками, проблемами), без которого в начале XXI невозможно представить шахматный мир. А ведь еще менее 40 лет тому назад шахматисты, встречаясь, не задавали друг другу вопрос “Каков Ваш Эло?”, не ждали очередного рейтинг-листа FIDE, чтобы выяснить свой новый коэффициент, узнать об изменениях в первой десятке, сотне лучших (по  вычислениям составителей этого листа) своих коллег. Конечно, различные способы ранжирования спортсменов были и раньше во многих видах спорта- определялись лучшие из лучших в стране или в мире за год, за десятилетие. В большинстве ситуаций  ранги приписывались спортсменам в соответствии с занятыми местами и показанными результатами. Были даже попытки сравнивать представителей различных видов спорта (в первую очередь – легкой атлетики), создавая для этого специальные таблицы для пересчета, скажем, долей секунд в женском беге на сто метров в сантиметры мужчин - толкателей ядра. В шахматах тоже была своя иерархия- чемпион мира, ближайшие претенденты на соискание этого звания, ведущие (но не претендующие на чемпионство) гроссмейстеры, международные мастера, национальные мастера и так далее. Раз в 3 года шахматный мир следил за очередными попытками (успешными или безуспешными) шахматиста номер два, называемого  “претендентом на шахматную корону”,  поменяться местами с чемпионом мира – первым номером в классификации FIDE. “Претендент” - титул, завоеванный в результате отбора, в котором мог участвовать через сито национальных чемпионатов, зональных и межзональных турниров, матчей претендентов формально любой шахматист, но, как правило, реально претендовать на него мог только узкий круг сильнейших гроссмейстеров.  Что же касалось последующих ( третьего, четвертого,… ) номеров в шахматном мире, то они ни за кем официально или неофициально не закреплялись. Разве что третьим мог быть назван проигравший в финале претендентского цикла – он имел льготы в следующем цикле. Шахматная элита, встречаясь в международных турнирах, могла еще выяснить личные взаимоотношения, а уж сравнить уровень мастеров средней руки даже из таких развитых шахматных стран, как СССР и США,  было практически невозможно (разве что по принципу : “ мастер X в чемпионате США проиграл гроссмейстеру Бенко, а мастер Y в полуфинале первенства СССР сделал ничью с гроссмейстером Z, который, в свою очередь, уже в финале сыграл вничью с Михаилом Талем, а тот в турнире претендентов 1959 года в Югославии взял у Бенко 3,5 очка из 4, следовательно, Y должен стоять выше”).  Да и даже, если соперники ( скажем, A, B и C ) имели возможность часто встречаться друг с другом, было трудно расставить их по силе, если , например, A регулярно выигрывал у B, но всегда имел проблемы в партиях с С, которому, в свою очередь, не везло с В (таких примеров имеется множество в шахматной истории). Несмотря на это, вопросы типа “ кто же был сильнее в свои лучшие годы - Александр Алехин, Михаил Ботвинник или Роберт Фишер?” задавались довольно-таки часто и даже делались попытки привлечь для ответа на такие вопросы различные статистические материалы. Такого рода попытки сравнивать представителей различных эпох и континентов привели к появлению в XX веке первых рейтинговых систем, которые использовались в отдельных странах, а одна из них – система индивидуальных коэффициентов Арпада Эло- была в 1970 году официально принята FIDE для сравнения результатов шахматистов.

За прошедшие три с лишним десятка лет системой ЭЛО охвачены  десятки тысяч шахматистов различной квалификации, большинство из которых не имели и не имеют практических шансов сыграть друг с другом, но объединенные единым рейтинг- листом могут воскликнуть “Gensunasumus!”. Возможно, что широкое распространение этой системы в конце прошлого века было вызвано и тем, что авторитет матчей на первенство мира (и как следствие- новоявленных чемпионов мира) перестал быть непререкаемым  после ухода непобежденного Роберта Фишера из шахмат, политизированных поединков Виктора Корчного с Анатолием Карповым, появления конкурирующих шахматных федераций и ассоциаций со своими чемпионами, отказывающимися встречаться друг с другом, и тем, что шахматы быстро перешли на  коммерческие рельсы. Все это привело к необходимости иметь способ количественной оценки результатов шахматистов и их потенциальных возможностей. Нужна была система, способная определить, кто из многочисленных действующих (по разным версиям) чемпионов мира является действительно сильнейшим. Спонсоры многочисленных коммерческих турниров также хотели приглашать в эти турниры действительно лучших (по каким-то признанным стандартам) игроков. Система коэффициентов Арпада Эло стала официальной системой FIDE. Однако в ряде федераций были приняты несколько иные оценки результатов входящих в эти федерации игроков. Эти системы (например, рейтинг USCF)  в той или иной мере коррелированы с рейтингом ЭЛО. Среди шахматистов, входящих в верхнюю часть рейтинг- листа, популярен и профессиональный рейтинг ( несколько отличающийся от рейтинга ЭЛО),  система которого была разработана Кеном Томпсоном. Имеется и ряд других систем (например, Glicko и Glicko-2, предложенные профессором Гликманом ( M.E. Glickman)), авторы которых пытаются улучшить официальную рейтинг-систему FIDE. Мы рассмотрим различные достоинства и недостатки системы ЭЛО и попытаемся наметить пути ее улучшения. Отметим, что имеется ряд взглядов на проблемы ранжирования силы шахматистов, некоторые из которых мы поддерживаем, а с некоторыми принципиально не согласны.  Ниже мы постараемся подкрепить наши рассуждения теоретико-вероятностными и статистическими аргументами.

 

2.Основные требования к рейтингам

 

            Любая система рейтингов – это попытка ранжировать действующих шахматистов, основываясь на их результатах. Конечно, интересно было бы получить не только места, занимаемые конкретными игроками в длинном списке участников многочисленных соревнований, но и попытаться количественно отобразить на какой-либо шкале шахматную силу сравниваемых шахматистов. Более того, система должна быть достаточно динамичной, чтобы быстро отображать изменения, происходящие в шахматном мире. В то же время система должна содержать элементы устойчивости – в ней должны быть выделены некоторые абсолютные (фиксированные или не меняющиеся на длительном временном промежутке) уровни, служащие ориентирами для разбиения шахматистов на определенные категории. Причем, если для лучших 50-100 шахматистов важно, как количественно соотносятся их рейтинги, то для основной массы шахматистов представляет интерес, в какой кластер попадает их рейтинг, и какова его динамика за последнее время. Не так важно, например,  кто занимает перед тобой в списке место под номером 5345 (это если и можно определить, то с громадным трудом, переработав большой лист данных, составленный в алфавитном порядке), а существеннее, сколько тебе осталось до отметки 2400 или насколько прибавилась за последние три месяца твоя шахматная сила. Для организаторов соревнований важно, чтобы большая часть участников имела бы официальные рейтинги и желательно, чтобы среди этих рейтингов не было бы одинаковых. С увеличением числа игроков, получивших рейтинг, увеличивается вероятность появления шахматистов, имеющих совпадающий рейтинг. Поэтому, если, например, в первых рейтинг – листах ЭЛО значения округлялись до 5 очков, то теперь FIDE использует округление до одного очка, но и это не избавляет от появления одинаковых рейтингов. Скажем, даже в сравнительно разреженной верхней части последнего листа FIDE среди первых 50 его участников двое имеют рейтинг 2687, двое- 2682, еще двое делят 26-27 места с результатом 2676, по три шахматиста остановились на уровнях 2669 и 2663, два гроссмейстера имеют результат 2660. Возможно, в дальнейшем придется проводить вычисление рейтингов с одним или двумя десятичными знаками, чтобы “отделить” шахматистов друг от друга. Это важно не для того, чтобы увеличить точность вычислений, а для того, чтобы избежать некоторой неопределенности при распределении участников соревнований по группам, а также более эффективно использовать рейтинговый фактор при равенстве прочих показателей.

Создатели некоторых систем претендуют на то, чтобы, пользуясь базой данных, проводить “обратный отсчет” и сравнивать рейтинги действующих и давно уже сошедших со сцены шахматистов.  Представляется, что этот подход достаточно искусственный. Таким образом пытаются ответить на вопрос типа “кто кого поборет- кит слона или слон кита?”. Дело в том, что в цепочках партий A против B, В против С, С против D,..., X против Y, Y против Z, используемых, чтобы от шахматиста A начала XXI века добраться до шахматиста Z, игравшего в конце XIX века,  хоть и фигурируют одинаковые имена (В и В, С и С,...),  но ,по существу, это разные по силе шахматисты, и в результате таких вычислений накапливаются большие погрешности. Более того, даже один и тот же шахматист, имеющий , скажем, рейтинг 2700 , может быть безусловным лидером шахматного мира в 1980 году и с тем же рейтингом даже не входить в десятку лучших шахматистов через 20 лет. Этот эффект можно объяснить следующим образом. Представьте, что на некоторый интервал случайно бросают n точек. С ростом n эти точки все плотнее заполняют интервал и крайние (как справа, так и слева) точки все ближе и ближе приближаются к концам выбранного для заполнения интервала, хотя при этом среднее арифметическое значение всех координат может иметь постоянную величину. В соответствии со сказанным, максимальное, десятое, сотое значения рейтинга должны  расти с ростом числа шахматистов, получивших рейтинг. Поэтому не совсем удачными представляются системы, в которых предлагается бороться с  “инфляцией” максимальных рейтингов, сдвигая шкалу таким образом, чтобы, скажем, рейтинг десятого по силе игрока оставался постоянным, например, равным 2700. Более естественным было бы говорить о существовании  “инфляции”, наблюдая за динамикой так называемых “одно-процентных точек”, т.е. рейтингами пятидесятого номера в рейтинг-листе при 5000 шахматистов, имеющих рейтинг, семидесятого номера, когда этот лист увеличился до 7000 человек, сто двадцатого номера при 12000 шахматистов с рейтингом и так далее. Эти точки должны сохранять устойчивость, не меняясь заметно со временем. Аналогична ситуация с “двух-процентными”, ”трех-процентными” и так далее точками. Это объясняет тот факт, что  даже в случае отсутствия “инфляции” вполне естественной является ситуация, когда число шахматистов, имеющих, скажем, рейтинг 2400, растет пропорционально числу шахматистов, попавших в рейтинг лист. Поэтому не должен удивлять рост числа шахматистов, имеющих официальные звания FIDE, если получение таких званий связано с достижением некоторых определенных уровней рейтинга.

Приведенные доводы показывают, что можно, конечно, вычислять рейтинги Морфи, Стейница, Капабланки, но имеет смысл сравнивать эти рейтинги только с полученными таким же образом рейтингами их современников.

            Рассмотрим еще одно обстоятельство, играющее важную роль при обсчете рейтингов. Представьте, что все шахматисты разделены на несколько непересекающихся групп и соревнуются только внутри своих групп. Обсчет их рейтингов даст представление о взаимоотношениях внутри групп, но не позволит сравнить участников из разных групп. Доводя до абсурда ситуацию, можно рассмотреть двух шахматистов, которые играют только друг с другом. Если один из них будет постоянно выигрывать, он может неограниченно увеличивать свой рейтинг и превысить со временем даже рекордный на сегодняшний день рейтинг Гарри Каспарова, но это не значит, что этого игрока назовут сильнейшим в мире. Правда, можно возразить, что проигрывающий все свои партии партнер так же резко снизит свой рейтинг до минимально возможного уровня, выйдет из рейтинг-листа и перестанет поставлять рейтинговые очки своему более удачливому сопернику, но ведь есть же и системы (например, система USCF), в которых невозможно понизить свой рейтинг ниже некоторого определенного уровня. Поэтому в любом случае, если система претендует на существенную общность, она должна предусмотреть соответствующее “перемешивание” участников за сравнительно обозримый промежуток времени. Под “перемешиванием” мы как раз и понимаем ситуацию, при которой не образуются долговременные группы постоянных шахматистов, которые при этом не играют с другими участниками рейтинг – листа.

            Авторы различных систем в качестве одного из основных достоинств рассматривают возможность по рейтингу предсказывать результаты носителей рейтинга. Представляется спорным, что вероятность точного предсказания может быть близкой к единице. Скажем, если мы опираемся лишь на последний опубликованный рейтинг, то по его сути ожидаемые с наибольшей степенью достоверности  данные следующего рейтинг –листа должны полностью совпадать с предыдущим, а такие совпадения еще не встречались, да и возможны, пожалуй , лишь, если за очередные три месяца между последовательными публикациеями двух рейтингов не будет сыграна ни одна шахматная партия. Более точно можно предсказывать очередной рейтинг, если известно его долговременное поведение, которое позволяет получить полезную дополнительную информацию о рейтинге как о некотором случайном процессе. Но и в этом случае подобную информацию надо иметь о всех соперниках шахматиста, чей будущий рейтинг мы пытаемся предсказать. Можно попытаться предсказать результаты определенного шахматиста на протяжении некоторого временного интервала. Трудно это сделать, если речь идет об одной партии. Пусть, например, сравнение рейтингов двух соперников приводит к предсказанию, что A должен в партии с B набрать 75 процентов, т.е. наиболее правдоподобный результат должен быть 0,75 очка. Ясно, что любой истинный результат (0, ½  или 1) будет отличаться от предсказания не менее, чем на треть. Конечно, если попытаться предсказывать суммарный итог большого числа партий, то в этом случае ошибка подобного округления будет меньше. Можно привести еще ряд доводов, объясняющих, почему точность предсказания не может быть очень высокой. Любое значение рейтинга является некоторым усреднением уровня силы шахматиста. Этот уровень по различным причинам может меняться даже на протяжении одного сравнительно длительного турнира. А ведь часты ситуации, когда шахматист длительное время не играет, а его рейтинг остается все это время постоянным. Поэтому считать, что официальный рейтинг шахматиста отвечает его сегодняшнему уровню игры можно лишь с некоторой натяжкой. Долгое время рейтинг FIDE обсчитывался с округлением до 5 баллов, поэтому большинство партий в шахматных базах содержат данные о рейтинге игравших соперников с такой точностью. Отметим, что данное округление также дает некоторую погрешность, поскольку ожидаемое значение набранных очков при увеличении рейтинга на 5 баллов уже меняется на один процент. Существенно большую погрешность вносит система обсчета, в которой не учитывается цвет фигур соперников. Более подробно об этом мы поговорим ниже, отметив, что право выступки оценивается примерно в 40 рейтинговых очков ЭЛО (при равенстве рейтингов играющий белыми должен в среднем набирать не 50, а примерно 55 процентов очков). Значительно может меняться рейтинг в зависимости от периода времени, в течение которого набираются партии для очередного его пересчета (год, полгода, нынешние три месяца, берущиеся для пересчета официального рейтинга FIDE, месяц). Особенно заметно влияние данного фактора, когда у шахматиста на протяжении этого периода идет длинная серия успехов (или неудач), такая, например, какая сопровождала Роберта Фишера в его претендентских матчах перед завоеванием им чемпионского звания. Если бы его рейтинг  пересчитали уже после первого матча, выигранного со счетом 6:0, то результат 6:0 следующего матча был бы более ожидаемым и принес бы Фишеру существенно меньшую прибавку рейтинга. Поэтому, если есть технические возможности, рейтинг следует пересчитывать после каждой партии (это в идеале) или хотя бы раз в неделю. Конечно, пересчет “после каждой партии” можно провести не обязательно в день, когда играется партия, а сразу после окончания турнира.  Все эти аргументы показывают, что гнаться за высокой степенью точности предсказания будущих результатов, опираясь на имеющийся  рейтинг, не имеет большого смысла. Статистические выводы, приведенные авторами некоторых новых рейтинг- систем и критиками старых, показывают, что лучшие с точки зрения прогноза системы обеспечивают точность предсказания будущих результатов около 85 процентов. Одной из дискутируемых проблем, связанных с подсчетом рейтинга, является вовлечение в этот обсчет партий с разным контролем времени. Многими авторами предлагается рассматривать все партии, сыгранные данным шахматистом за отчетный период, но включать их в рейтинг с разными коэффициентами. Скажем, если классические партии берутся с коэффициентом единица, то “30-минутные” партии, как предлагает, например,  Джефф Сонас, надо учитывать с коэффициентом 0,29, а “пятиминутки”, по его мнению, должны вносить свой вклад в рейтинг шахматиста с весом 0,18. Мотивируется необходимость учета всех партий тем, что любая из них несет определенную информацию о силе шахматиста, и эта информация должна влиять на рейтинг. Представляется, что все-таки роли классических и блиц партий в истории шахмат существенно различаются. Вряд ли кто-то сейчас припомнит хоть один фрагмент из блиц – партий , сыгранных Михаилом Талем, блестяще игравшим и классику и блиц, а его “классическому” творческому наследию посвящены многие тома, хотя, по мнению того же Джеффа Сонаса, 6 партий, сыгранных соперниками за час, эквивалентны одной партии, сыгранной с классическим контролем времени. Мне могут возразить, что в теннисных рейтингах одинаково ценятся матчи, сыгранные на травяных и грунтовых кортах, а в легкой атлетике специально подобранная система очков позволяет определять победителя в десятиборье, где спортсмены соревнуются в дисциплинах, отстоящих друг от друга на существенно большем расстоянии, чем “классические” и “быстрые” шахматы. Что касается тенниса, там существует отработанная система турниров, практически обязательных для всех спортсменов из верхней части рейтинг - листа. Все теннисисты находятся в равных условиях, выступая примерно в одинаковом числе соревнований, проводимых на различного типа кортах. Многоборье представляет особый вид легкой атлетики, в котором успеха, как правило, добиваются спортсмены, показывающие высокие, но не выдающиеся результаты в отдельных видах этого многоборья. Можно было бы устраивать и некоторый аналог шахматного многоборья, объединив в одном турнире, скажем, классические и блиц- шахматы с бриджем и бильярдом, но это тоже будем другим видом единоборств. Тем не менее, учитывая, что процент шахматных партий, играемых с классическим контролем времени, уменьшается с каждым годом, да и в матчах, проводимых по классическим правилам, для определения победителя при их ничейном исходе регламент предлагает играть “быстрые” партии , следует подумать о гибкой системе обсчета рейтинга, при которой будут учитываться не только партии с классическим контролем, но и все партии с каким-то разумным (например, не менее полутора часов на партию) контролем. 

 

3. Математические модели систем шахматных рейтингов

 

            Выше уже отмечалось, что существуют различные варианты ранжировать шахматистов по уровню их игры. Наиболее распространенной является принятая FIDE система Арпада Эло. Ряд других систем представляют собой те или иные модификации рейтинга ЭЛО. Рассмотрим некоторые математические основы построения таких систем.

 Более 50 лет тому назад была предложена одна из первых систем упорядочивания шахматистов. Она называлась Инго- система ( Ingo-system) в честь баварского города Инголштадт (Ingolstadt) –родного города автора этой системы  Антона Хесслингера ( Hoesslinger). Суть этой системы была в следующем. Рейтинг шахматиста пересчитывался или впервые устанавливался на основе сыгранных им за некоторый соревновательный период партий. Брался в расчет средний рейтинг R_ср его соперников в этих партиях   и процент Π (0≤ П      ≤ 100) набранных в этих партиях очков. Тогда новый рейтинг R определялся по формуле

 

R=R_ср +(50-Π).                                                                                (1)

Отметим, что эта система приписывала более низкий рейтинг более сильному игроку. Предыдущий рейтинг игрока не учитывался в его новом рейтинге, но учитывался при подсчете R_ср для его соперников. Соотношение (1) было простым, но его недостатком была слишком большая зависимость рейтинга от результата нескольких последних партий. Важным фактом, использованным впоследствии большинством других систем, была зависимость нового рейтинга от среднего рейтинга соперников и разности между достигнутым результатом и некоторым ожидаемым результатом шахматиста (в Инго-системе ожидаемым считался 50-процентный результат).

            Следующий важный шаг к созданию ныне действующей официальной системы FIDE был сделан Арпадом Эло (ArpadElo). Он учел, что сила шахматиста даже на протяжении одного соревнования не есть постоянная величина, а зависит от многих случайных факторов. Эло предложил каждому шахматисту сопоставить случайную величину ξ, имеющую нормальное (или, как еще говорят в теории вероятностей, гауссовское) N(R,σ) распределение с математическим ожиданием R и среднеквадратическим отклонением (rootmeansquaredeviation) σ = 200, где R совпадает с рейтингом данного игрока. Большое значение среднеквадратического отклонения, соответствующего дисперсии (variance) σ²= 40000, было выбрано из соображения удобства расположить на числовой оси большое число ранжируемых шахматистов. 

            Рассмотрим двух шахматистов, уровень игры которых описывается случайными величинами   ξ₁ ~  N(R₁ ,σ) и ξ₂ ~  N(R₂, σ), где R₁ и  R₂- их рейтинги. Эло сделал предположение, что в такой ситуации первый из шахматистов должен в игре со вторым набрать долю очков, совпадающую с вероятностью события { ξ₁> ξ₂}={ ξ₁- ξ₂>0}. Доля очков второго игрока, набранных  в игре с первым, будет совпадать уже с вероятностью события { ξ₂> ξ₁}={ ξ₁- ξ₂<0}. Отметим, что, наверное, такая идея больше подходит играм, в которых возможен лишь один из двух результатов- победа или поражение, но Эло распространил этот принцип и на шахматы, где, как известно, большая часть поединков заканчивается вничью. По таблицам, дающим значения функции распределения нормального закона, можно найти нужные вероятности при различных значениях разности рейтингов Δ=R₁-R₂.

Действительно,  если предположить, что ξ₁ и ξ₂ –независимые случайные величины, имеющие нормальные N(R₁ ,σ) и  N(R₂, σ) распределения, то , как известно, разность этих величин η= ξ₁ - ξ₂ имеет также нормальное распределение с математическим ожиданием, равным Δ=R₁-R₂ и дисперсией 2σ², т.е. среднеквадратическим отклонением 

σ₀= σ=200≈282,8. Если обозначить через ν стандартную нормальную случайную величину с нулевым математическим ожиданием и единичной дисперсией- именно ту, на  которую ориентированы соответствующие таблицы, то можно воспользоваться тем, что

η    имеет такое же распределение, что и величина σ₀ ν+ Δ. Тогда

 

P{ ξ₁> ξ₂}=P{ ξ₁- ξ₂>0}=P{ σ₀ ν+ Δ>0}=

           

P{ ν>- Δ/ σ₀}=P{ ν< Δ/ σ₀}=Φ(Δ/ σ₀),                                                   (2)

 

где Φ(x) –функция распределения стандартного нормального закона, таблицы которой достаточно широко распространены. Используя эти  таблицы, при различных Δ легко можно найти нужные нам вероятности. Например, если Δ=20, то Δ/ σ₀=1/10≈0,07 и

 

                                   P{ ξ₁> ξ₂}≈ Φ(0,07) ≈0,53.

 

Это по Эло означает, что первый игрок, имеющий рейтинг на 20 пунктов больший, должен во встречах со вторым набирать 53 процента возможных очков, оставляя 47 процентов на долю второго. Такие значения были найдены для широкого спектра значений  Δ. Параллельно Эло  подготовил как бы обратные таблицы. Приведем соответствующий пример. Пусть нас интересует такая разность рейтингов Δ, при которой первый шахматист должен набирать во встрече со вторым 84 процента очков. Это значит, что нужно найти такое значение Δ, при котором правая часть (2) обращается в 0,84.  По тем же таблицам нормального распределения находим, что

                                           Φ(x*)=0,84,

если x*≈1, а тогда уже Δ находим из соотношения

 

Δ/ σ₀=1

и получаем, что  Δ≈283. Таким образом, чтобы шахматист во встречах с соперником набирал 84 процента очков, нужно, чтобы его преимущество в рейтинге было порядка 280 пунктов. Таким образом, по новым таблицам каждому значению  p=0,50 (0,01) 0,99 сопоставляется разница в рейтинге соперников, которая должна обеспечивать первому из них долю очков p  во встречах со вторым. Если p<0,50, то достаточно поменять шахматистов местами и искать значение Δ, соответствующее уже 1-p.

            Подготовив две таких таблицы, Эло предложил следующую систему пересчета рейтинга по итогам партий , сыгранных за определенный срок (год, полгода, три месяца). Считаем средний рейтинг всех соперников R_ср и разность Δ=R- R_ср  обсчитываемого игрока и его усредненного соперника. По первой таблице находим ожидаемую долю очков p,  которую игрок должен был бы набрать во встрече с усредненным противником. Далее эта доля очков сравнивается с долей реально набранных очков p_N (можно сравнивать также не доли очков, а брать разность между ожидаемым и набранным числом очков – одна разность легко выводится из второй, если мы знаем число сыгранных партий). Напомним, что в Инго-системе в качестве ожидаемой доли бралась величина 0,50. Конечно, можно было бы (примерно, как в Инго-системе) просто взять в качестве исходного материала процент p_N , по этому проценту, используя вторую таблицу,  найти то значение Δ_N, которое обеспечивает такой результат, и в качестве нового рейтинга взять R_N=R_ср+ Δ_N. Такой подход был бы недостаточно гибким и резко менял бы последовательные рейтинги от пересчета к пересчету. Эло предложил как бы брать с некоторыми весами  старое R и новое R_N  значения  рейтингов, причем это можно делать, даже не вычисляя R_N, а опираясь на разность очков, набранных и ожидаемых, или долей очков, набранных и предсказанных. Для этого можно использовать формулу

 

R_New=R+K(p_N-p),                                                                       (3)

где R_New и R –соответственно  новый и старый рейтинги, p_N и p –набранный и ожидаемый проценты очков, а K – некоторый коэффициент, выбор которого может зависеть от числа партий , сыгранных за обсчитываемый период , и числа тех партий, на которых основывался старый рейтинг, от уровня старого рейтинга ( одно значение K, если, например, R>2400, и другое, если R<2400 и т.д.). Выбор коэффициента позволяет сделать рейтинг более или менее динамичным. Напомним, что в формуле (3) можно разность  

p_N-p заменить на соответствующую разность набранных и предсказанных очков. Коэффициент К может зависеть от числа или от доли сыгранных за некоторый период партий, помогая последним партиям внести в рейтинг больший или меньший вклад.

       Такова примерно структура многих рейтинговых систем. В некоторых из них есть свои специфические стороны. Так, например, в Профессиональном рейтинге или в Glisco-системе степени разброса значений рейтинга (то, чем в системе Эло является среднеквадратическое отклонение) не остаются постоянными, а меняются со временем. В системе USCF (Американской шахматной федерации) имеются некоторые пороги, ниже которых рейтинг шахматиста не может опуститься. Так, если кто-то достиг однажды рейтинга 2450, то уже ниже порога 2200 он не опустится.  Выше мы уже отмечали достоинства и недостатки рейтингов типа Эло.  Одна из проблем состоит в том, что система Эло не учитывает цвет фигур шахматиста, который оказывает существенную роль на исход партий, давая белым даже при одинаковых рейтингах соперников преимущество в 40-50 рейтинговых очков. Эта система, как мы отмечали выше, в какой-то степени игнорирует возможность ничьих. Эти факторы могут оказаться существенными там, где даже небольшие искажения рейтинга могут повлиять на ранжирование соперников. Речь идет, в первую очередь, о 50-100 лучших шахматистов мира. Предлагаем небольшие изменения, которые, по нашему мнению, помогли бы уменьшить влияние указанных недостатков.

            Рассмотрим некоторые статистические данные, показывающие преимущество белого цвета. Данные подготовлены Владимиром Балакиревым на основе результатов партий за период с 1998 по 2004 г., взятых из MegaDatabase . Рассматривались величины

T(R_w,R_b)=(N_w-N_b)/N, где N_w- число партий, выигранных белыми, N_b- выигранных черными и N- общее число партий, с фиксированной разностью рейтингов шахматистов, игравших белыми (R_w) и черными (R_b).  Величины R_wи R_b  последовательно фиксировались на уровнях 2300, 2310, 2320,…,2600, подбирались по базе партии, в которых игравший белыми имел рейтинг R_w, а рейтинг черных был равен R_b. По результатам всех этих партий находились величины T(R_w,R_b). Надо было отследить, при какой разности рейтингов значение T(R_w,R_b) (а эта величина совпадает с разностью долей очков, полученных  соответственно белыми и черными во всех партиях, сыгранных противниками с данными рейтингами) становится отрицательной.  Например, значения

 

T(2300,2300)=0,029; T(2300,2310)=0,003; T(2300,2320)=0,014;

T(2300,2330)=0,015; T(2300,2340)=0,009 T(2300,2350)= -0,023;

 T(2300,2360)= -0,002; T(2300,2370)= -0,0041

 

показывают, что преимущество черных в 40 рейтинговых пунктов еще не обеспечивает им

преимущества над белыми, а при 50 пунктах разницы это преимущество уже ощущается.

При рейтинге белых 2400 такое явление происходит между 30- и 40- очковой разностью:

T(2400,2430)=0,001 ,     а T(2400,2440)= -0,011.  Далее, T(2500,2530)=0,002, а T(2300,2340)=-0,012  и т.д. При всех значениях R_w было заметно, что переход от преимущества белых к преимуществу черных происходит в интервале от 30 до 50 пунктов разности рейтингов.  Чтобы более рельефно отразить этот момент, были собраны в одну группу все партии с фиксированными разностями рейтингов Δ=0,10, 20, … (причем они не подразделялись по рейтингу белых) и сосчитаны аналогичные T(R_w,R_b) значения (обозначим их T(Δ)). Получили, что T(0)=0,033, T(10)=0,014, T(20)=0,018, T(30)=0,006, T(40)= -0,08,  T(50)= -0,015, T(60)= -0,018, T(70)= -0,031, т.е. и здесь статистика показывает, что критическое значение разности рейтингов находится около значения 40. К сожалению, более точных статистических выводов сделать нельзя, поскольку в большинстве партий, используемых при подсчетах, указывался рейтинг с точностью до 5 пунктов ( рейтинг Эло долгое время округлялся именно с такой точностью). Поэтому будем  считать, что Δ=40   приближенно соответствует тому преимуществу, которое обеспечивает белый цвет фигур. Мы придем к этому значению Δ другим способом , используя несколько иные статистические выводы.

            Выше уже говорилось, что уровень шахматиста в конкретной партии (или даже на протяжении некоторого периода времени) Эло предложил представлять в виде  нормально распределенной случайной величины, математическое ожидание которой характеризует рейтинг шахматиста. В какой-то степени такое представление можно использовать, поскольку шахматная партия складывается из достаточно большого числа случайных взаимодействий, каждое из которых может принести некоторое микро – преимущество тому или иному сопернику. Из теории вероятностей известно (этот факт носит название  центральной предельной теоремы), что суммы большого числа случайных слагаемых хорошо приближаются случайными величинами, имеющими нормальное приближение. Каждый из игроков может в данной партии сыграть лучше или хуже своего среднего уровня и даже игрок, у которого рейтинг (среднее значение) ниже рейтинга своего соперника, имеет шансы показать более высокий уровень игры, чем его противник.  

Возвращаясь к идее Эло, предположим, что уровень игры соперников описывается случайными величинами   ξ₁ ~  N(R₁ ,σ) и ξ₂ ~  N(R₂, σ), где R₁ и  R₂- их рейтинги. Параметр  σ носит масштабный характер ( в чем измерять результат- в метрах, ярдах или сантиметрах?), для ранжирования шахматистов он не очень существенен и выбирается лишь из соображения удобства (как мы помним, у Эло   σ=200). В системе Эло ожидаемая доля очков, которую получит первый игрок в игре со вторым, определялась просто, как вероятность того, что    ξ₁> ξ₂ , т.е. первый из шахматистов сыграет, хоть ненамного, но лучше, чем его соперник. На самом деле, порой, даже большого, на первый взгляд, преимущества, достигнутого в партии одним из противников, не хватает для победы. Это означает, что для победы нужно не только превзойти соперника, но и превзойти достаточно существенно. Поэтому сделаем предположение, что для победы первого игрока нужно, чтобы произошло не событие  {ξ₁- ξ₂>0},  а событие {ξ₁- ξ₂>δ},  где  δ обозначает уровень накопленного преимущества, уже достаточного для победы. С помощью статистических процедур найдем значение δ. Введем в наши расчеты еще одну неизвестную величину Δ, которой мы будем обозначать то преимущество черных в рейтинге, которое может нейтрализовать право первого хода их соперника. Пусть  ξ₁ определяет силу белых, имеющих рейтинг R₁, а  ξ₂ – уровень черных с их рейтингом R₂ . С учетом цвета реальная разность рейтингов равна R₁-R₂+ Δ  и , сравнивая с формулой (2), можно выписать выражение для вероятности победы белых:

 

P{ ξ₁- ξ₂+ Δ > δ }=P{ σ₀ν+ R₁-R₂+ Δ> δ }=

           

P{ ν> (δ - Δ –( R₁-R₂))/ σ₀}=P{ ν<( R₁-R₂ -δ + Δ ) / σ₀}=

 

Φ(( R₁-R₂ -δ + Δ ) / σ₀),                                                                                (4)

 

где

σ₀=200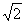≈282,8.

             

Аналогично получаем, что вероятность выигрыша черными имеет вид

P{ ξ₁- ξ₂+ Δ <- δ }= Φ(( R₂-R₁ -δ - Δ ) / σ₀),                                                (5)

 

а вероятность ничьей находится по формуле

 

                                                           P{ - δ <ξ₁- ξ₂+ Δ < δ }=

 

1- Φ(( R₁-R₂ -δ + Δ ) / σ₀)- Φ(( R₂-R₁ -δ - Δ ) / σ₀)=

 

Φ(( R₁-R₂ +δ +Δ ) / σ₀) - Φ(( R₁-R₂ -δ + Δ ) / σ₀).                             (6)

 

В соотношениях (4)-(6) фигурируют две неизвестные величины ( мы на время забыли о наших предыдущих выводах, связанных с оценкой Δ) и их можно определить статистическими приемами. Для простоты рассмотрим случай , когда белые и черные имеют одинаковый рейтинг (R₁=R₂).  MegaDatabase представила 8421 партию (за последние 6 лет), в каждой из которых рейтинг белых и черных совпадал (с точностью до округления). Из этих партий 2461 (или 29,2%) выиграли белые, а 1696 (или 20,1%) – черные. В правых частях (4) и (5) возьмем R₁=R₂ и полученные выражения приравняем 0,292 и 0,201 соответственно. Придем к равенствам

 

                                         Φ((Δ -δ ) / σ₀)=0,292       

и

                                        Φ((-δ - Δ ) / σ₀)=0,201.    

 

По таблицам функции распределения нормального закона находим теперь, что

 

                                               (Δ -δ ) / σ₀=-0,55

и

                                               (-δ - Δ ) / σ₀= -0,84.

 

Отсюда получаем, что Δ≈41, а δ≈197. Разумное округление позволяет считать, что преимущество первого хода действительно можно оценивать примерно в 40 рейтинговых очков в системе Эло, а для того, чтобы один шахматист выиграл у другого, он должен добиться в партии преимущества, оцениваемого примерно в 200 очков. Например, возьмем соперников, один из которых (играющий белыми) имеет рейтинг 2560, а второй – 2600. С учетом цвета фигур можно считать, что играют два равных противника с рейтингом 2600. Для того, чтобы найти вероятность выигрыша первого, нам надо для игроков с равным рейтингом вычислить вероятность  

 

              P{ ξ₁- ξ₂ > 200}.

 Она равна

1-Φ(200/ σ₀)=1- Φ(0,707) ≈0,24.

 

Такая же вероятность выиграть имеется у черных, а ничейный исход можно предполагать с вероятностью 0,52. Естественно в этом случае мы будем ожидать, что оба наберут по 50% очков. В системе же Эло ожидаемый результат игрока с рейтингом меньшим на 40 рейтинга противника равен 44 процентам, а его противник (хоть он и играет черными) должен набирать 56 процентов. Таким образом возможности черных завышены более чем на 10 процентов (вместо 50 им ставится задача получить 56 процентов).Таким образом, если учитывать цвет, то победа и ничья черных будет оцениваться ( с точки зрения приращения рейтинга)  выше, чем аналогичные результаты белых.

            Конечно, приведенные значения   Δ и  δ получились в результате статистической обработки большого набора партий, в которых рейтинг игроков пробегал широкий диапазон – от 2300 до 2700. Если ограничиваться более ровным составом участников нашего статистического исследования, например, игроками, чей рейтинг лежит в более узких полосах 2300-2400  или  2700-2800, то значения интересующих нас параметров могут меняться, хотя и не очень существенно, от диапазона к диапазону. В какой-то степени это связано с используемым в некоторых рейтинговых системах предположением, что дисперсия (степень разброса) уровня игры и результатов шахматистов уменьшается при увеличении рейтинга игроков. Это может отразиться на том, что среднеквадратическим отклонением рассмотренных нами выше разностей  ξ₁- ξ₂ будет не  σ₀=200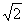≈ 283, а меньшая величина. Эта гипотеза требует более тщательной проверки.

            Уже многие шахматисты соглашаются с тем, что следует по отдельности оценивать при пересчете рейтинга результаты, достигнутые белыми и черными фигурами. Мы надеемся, что предложенная нами (как нам кажется, более справедливая) система подсчета ожидаемых результатов при игре белыми и черными не потребует существенной перестройки существующих принципов ранжирования игроков.